Naturaleza exacta

   Leonardo de Pisa, más conocido como Fibonacci, fue un matemático italiano al cual debemos entre otras cosas que hoy día usemos el sistema de numeración indo-arábigo (1, 2, 3, 4, 5...) sin el cual, seguiríamos escribiendo en números romanos (I, II, III, IV, V...). Trajo a Europa los conocimientos matemáticos árabes, entre ellos esta curiosa serie de números de la que trata esta entrada, a la que conocemos por sucesión de Fibonacci. 

   Dicha sucesión, hace referencia a una serie infinita de números, los cuales se consiguen al ir sumando a cada número los dos anteriores. La serie empezaría por el 0 y el 1, que al sumarlos volvería a dar 1. Así obtendríamos los tres primeros números (0, 1, 1). Si continuamos sumando las dos últimas  cifras (1, 1) daría 2, por lo tanto la serie seguiría 0, 1, 1, 2... y si seguimos sumando siempre los dos últimos números iríamos obteniendo la siguiente serie:

1, 1, 2, 3, 5, 8, 13, 21, 34...

   Viendo estos números, aquí viene la primera curiosidad relacionada con ellos. Si cortamos un plátano por la mitad, veremos que se divide en 3 secciones; si cortamos una manzana veremos que en 5 o si contamos los pétalos de una flor, las podremos encontrar de 1, 3, 5, 8, 13, 21... resulta sorprendente pero esta serie de números se repite constantemente en la naturaleza y no es por casualidad.

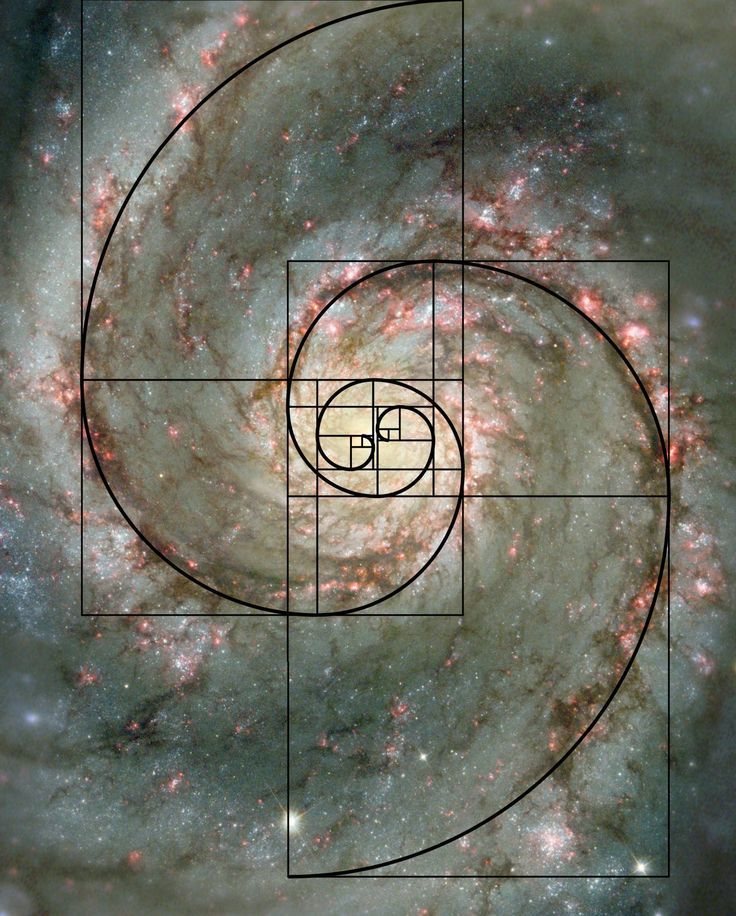
   Pero aquí no acaba la cosa, sí vamos creando cuadrados con el lado del tamaño de estos números y trazamos una línea uniendo sus esquinas, obtendremos una figura tal que así:

   Y aquí viene otro dato curioso de todo esto y es que esta forma, de nuevo se repite en la naturaleza una y otra vez. La cáscara de los caracoles, las hojas de una palmera, una estrella de mar, las pipas de un girasol, una galaxia en espiral... todo sigue este patrón matemático con increíble exactitud.

   Pero aquí no acaba lo asombroso de todo esto. Si cogemos cualquiera de los números de esta sucesión y lo dividimos por su anterior, nos dará como resultado un número aproximado a 1,6. A este número, representado desde la antigua Grecia como “phi” (Φ) , se le conoce como el “número de Dios“ o “número Áureo”, y se ha asimilado desde la antigüedad a la perfección y a la belleza. ¿Qué tiene este número de especial para que le llamaran así? Pues de nuevo es un número que se repite en la naturaleza una y otra vez. Solo basta con fijarse en el cuerpo humano y este número aparece por todas partes. Por ejemplo si dividimos nuestra altura total por la altura que hay hasta nuestro ombligo, dará 1,6. También lo encontraremos si dividimos la longitud de cada falange de los dedos de nuestra mano por la de la anterior.

 

   Se puede determinar si el útero de una mujer tiene un aspecto normal si al dividir su altura por su anchura, el resultado es cercano a 1,6. Pero también lo encontramos si dividimos la longitud de nuestro brazo desde hombro a los dedos con la que hay desde el codo, y lo mismo ocurre si lo hacemos con la longitud que hay desde la cadera a los pies dividida entre la que hay desde las rodillas. También lo encontramos en la relación entre el diámetro de la boca y el de la nariz, incluso aparece relacionado en otros órganos del interior del cuerpo humano como la tráquea, los bronquios o nuestro corazón. Todo siempre da 1,6, por eso siempre se le ha relacionado con el número De Dios.

   Pero no solo se encuentra en el cuerpo humano. El número áureo podemos encontrarlo por todas partes en el reino animal. Por ejemplo, en las abejas la medida del abdomen dividida por 1,6 es igual a la medida de su tórax y a su vez, la medida del tórax dividida por 1,6 es igual a la medida de su cabeza.

En el siglo XVI, un matemático italiano llamó a este número La Divina Proporción, debido a la belleza visual que genera al ojo humano cualquier elemento con proporciones áureas. Como hemos visto, la naturaleza está plagada misteriosamente de esta perfecta proporción, la cual es conocida y usada por los hombres desde hace miles de años. Podemos encontrarla en creaciones humanas desde las pirámides de Egipto al Partenón de Atenas, o desde la Mona Lisa hasta las tarjetas de crédito o las cajetillas de tabaco que existen en la actualidad.

Hay estudios que demuestran que una persona nos parece más atractiva cuanto más cercanas sean sus facciones físicas a la proporción áurea. ¿Algunos de ustedes tiene cara de caracol? ;)